기억보다 기록을
레저버 옵저버 (Reservoir observer) 실습 (MATLAB) 본문

논문의 예제처럼 Lorenz system에서의 Reservoir Computing (RC)를 MATLAB으로 구현해보려고 한다.
코드의 전체적인 구성은 다음과 같다.
- 샘플 데이터 생성 및 정규화
- RC 모델 구축 (행렬 \( A, W_{in}\ 등)
- Ridge regression을 통해 \( W_{out}\) & \(c \) 계산
- \( s(t) \) 추론 및 시각화
1. 샘플 데이터 생성 및 정규화
Lorenz system의 샘플 데이터 생성 (초기조건 : \( (x(0),\,y(0),\,z(0)) = (1,\,1,\,1) \) )
$$ \begin{aligned} \frac{dx}{dt} &= a(y - x), \\ \frac{dy}{dt} &= x(b- z) - y, \\ \frac{dz}{dt} &= xy - c z. \end{aligned} $$
clear; clc; close all;
%% 1. 샘플 데이터 생성 (Lorenz System)
a = 10; b = 28; c = 8/3;
lorenz = @(t,s) [a*(s(2)-s(1)); ...
s(1)*(b-s(3))-s(2); ...
s(1)*s(2)-c*s(3)];
% ODE solver로 미분방정식 계산
dt = 0.02;
[t, raw_data] = ode45(lorenz, 0:dt:100, [1; 1; 1]);
이 예시에서 전체 데이터 길이는 5000인데, \( 1 \leq t \leq 1000 \)은 transient time, \( 1000< t \leq 4000 \) 은 train data, \( 4000 < t \leq 5000 \) 은 test data로 쓰려고 한다.
또한 이 예시에서는 \( x\)를 \( u(t) \)로 보고 \( y,\,z\)를 \( s(t) \)로 다룬다.
tau = 1000; % transient time
train_len = 3000;
raw_train_x = raw_data(1+tau:tau+train_len, 1);
raw_train_y = raw_data(1+tau:tau+train_len, 2:3);
raw_test_x = raw_data(1+tau+train_len:end, 1);
raw_test_y = raw_data(1+tau+train_len:end, 2:3);
각 데이터 정규화
% train, test data normalization
[train_x, mu_x, sigma_x] = zscore(raw_train_x);
[train_y, mu_y, sigma_y] = zscore(raw_train_y);
test_x = (raw_test_x - mu_x) ./ sigma_x;
test_y = (raw_test_y - mu_y) ./ sigma_y;
2. RC 모델 구축
input layer와 output layer 사이의 reservoir layer인 \( r(t) \in \mathbb{R}^N\) 에 대한 수식은 아래와 같다.
$$ \mathbf{r}(t + \Delta t) = (1 - \alpha)\mathbf{r}(t) + \alpha \tanh(\mathbf{A}\mathbf{r}(t) + \mathbf{W}_{in}\mathbf{u}(t) + \xi \mathbf{1}), $$
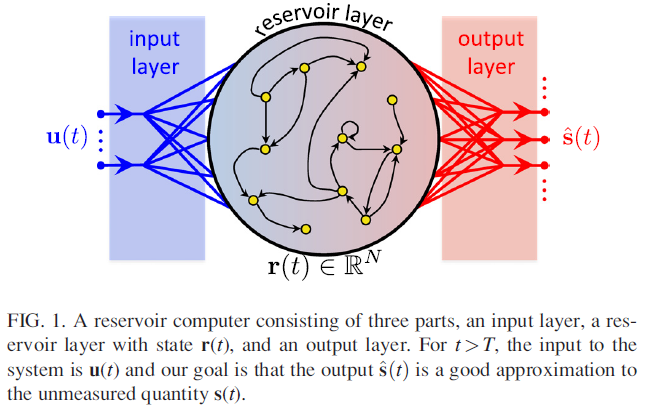
먼저 학습에 필요한 parameter와 행렬들을 정의한다.
%% 2. Reservoir 모델 구축
rng(42);
% parameter setting
N = 200; % number of reservoir nodes
alpha = 0.2; % Leakage rate
bias_scale = 1.0; % Bias term (xi)
input_dim = 1;
D_avg = 20; % average degree of reservoir node
Spectral_Radius = 0.95; % eigenvalue 의 절댓값의 최대치
sigma = 1.0; % W_in 에서 샘플링 range
논문의 방법대로 두 행렬을 생성
% 인접행렬 A 생성 및 정규화
A = full(sprand(N, N, D_avg/N));
A(A~=0) = (A(A~=0) - 0.5) * 2;
A = A * (Spectral_Radius / max(abs(eig(A))));
% W_in 생성 (Random Uniform [-sigma, sigma])
Win = (rand(N, input_dim) - 0.5) * 2 * sigma;
다음으로, \( r(t) \) 를 계산한다.
%% Reservoir state 계산
% r(t + dt) = (1 - alpha)*r(t) + alpha * tanh(A*r(t) + Win*u(t) + xi)
total_steps = size(train_x, 1);
states = zeros(total_steps, N);
r = zeros(N, 1);
for i = 1:total_steps
linear_part = A*r + Win*train_x(i, :)' + bias_scale;
r = (1-alpha)*r + alpha*tanh(linear_part);
states(i, :) = r';
endstates 행렬의 크기는 \( (샘플 데이터의 시간 길이) \times N \)이며, 각 행에는 시간에 따른 \( r(t) \)의 정보가 담겨있다.
3. Ridge regression을 통해 \( W_{out}\) 및 \( s(t) \) 추론

%% Delta_R, Delta_S 설정
beta_reg = 1e-8; % Ridge regression parameter
R_raw = states';
S_raw = train_y';
r_bar = mean(R_raw, 2);
s_bar = mean(S_raw, 2);
delta_R = R_raw - r_bar;
delta_S = S_raw - s_bar;
%% 출력 가중치 W_out* 및 c* 계산
% W_out* = delta_S * delta_R^T * (delta_R * delta_R^T + beta * I)^-1
term1 = delta_S * delta_R'; % (P x N)
term2 = (delta_R * delta_R') + (beta_reg * eye(N)); % (N x N)
W_out = term1 * inv(term2); % 역행렬 곱
% c* = - [W_out* * r_bar - s_bar]
c_star = - ( (W_out * r_bar) - s_bar );
4. \( s(t) \) 추론 및 시각화
test_states = zeros(test_len_actual, N);
for i = 1:size(test_x, 1)
% 1. Test 입력 가져오기
u = test_x(i, :)';
% 2. Reservoir 상태 업데이트 (학습 때와 동일한 식)
linear_part = A*r + Win*u + bias_scale;
r = (1-alpha)*r + alpha*tanh(linear_part);
% 3. 상태 저장
test_states(i, :) = r';
end
% 예측 수행
Y_pred = (W_out * test_states' + c_star)'; % (P x Test_Time)' -> (Test_Time x P)
시각화
%역변환
Y_pred_real = (Y_pred .* sigma_y) + mu_y;
% 결과 비교
figure('Position', [100, 100, 1000, 600]);
% y 변수 비교
subplot(2,1,1);
plot(raw_test_y(:,1), 'b', 'LineWidth', 1.5); hold on; % 원본 실제값
plot(Y_pred_real(:,1), 'r--', 'LineWidth', 1.5); % 역변환된 예측값
title('Inference of y');
legend('Real', 'Inferenced'); grid on;
xlabel('Time Step'); ylabel('y');
% z 변수 비교
subplot(2,1,2);
plot(raw_test_y(:,2), 'b', 'LineWidth', 1.5); hold on; % 원본 실제값
plot(Y_pred_real(:,2), 'r--', 'LineWidth', 1.5); % 역변환된 예측값
title('Inference of z');
legend('Real', 'Inferenced'); grid on;
xlabel('Time Step'); ylabel('z');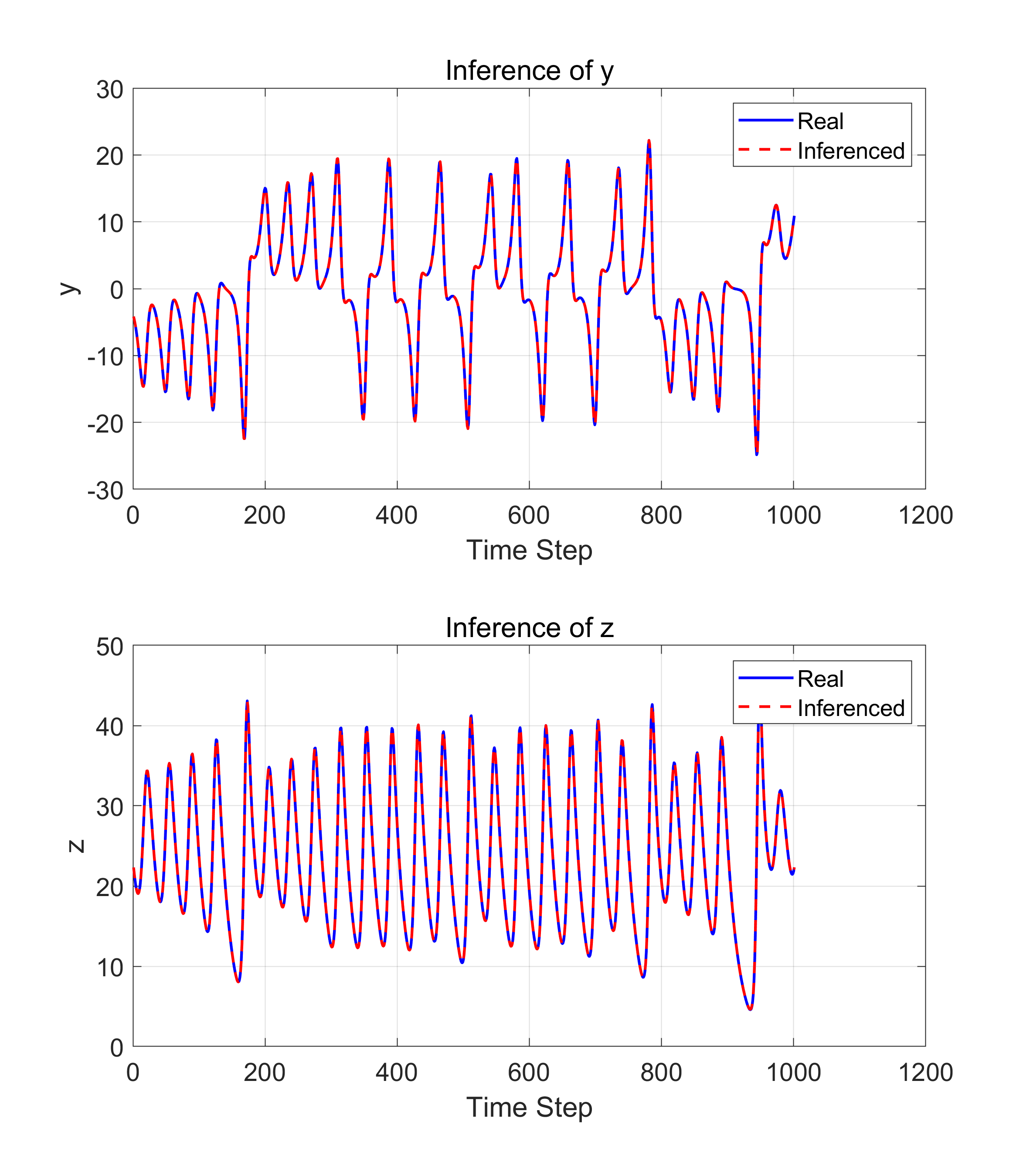

전체 코드
clear; clc; close all;
%% 1. 샘플 데이터 생성 (Lorenz System)
a = 10; b = 28; c = 8/3;
lorenz = @(t,s) [a*(s(2)-s(1)); ...
s(1)*(b-s(3))-s(2); ...
s(1)*s(2)-c*s(3)];
% ODE solver로 미분방정식 계산
dt = 0.02;
[t, raw_data] = ode45(lorenz, 0:dt:100, [1; 1; 1]);
tau = 1000; % transient time
train_len = 3000;
raw_train_x = raw_data(1+tau:tau+train_len, 1);
raw_train_y = raw_data(1+tau:tau+train_len, 2:3);
raw_test_x = raw_data(1+tau+train_len:end, 1);
raw_test_y = raw_data(1+tau+train_len:end, 2:3);
% train, test data normalization
[train_x, mu_x, sigma_x] = zscore(raw_train_x);
[train_y, mu_y, sigma_y] = zscore(raw_train_y);
test_x = (raw_test_x - mu_x) ./ sigma_x;
test_y = (raw_test_y - mu_y) ./ sigma_y;
%% 2. Reservoir 모델 구축 (Lu et al., Sec. II. SETUP)
rng(42);
% parameter setting
N = 200; % number of reservoir nodes
alpha = 0.2; % Leakage rate
bias_scale = 1.0; % Bias term (xi)
input_dim = 1;
D_avg = 20; % average degree of reservoir node
Spectral_Radius = 0.95; % eigenvalue 의 절댓값의 최대치
sigma = 1.0; % W_in 에서 샘플링 range
% 인접행렬 A 생성 및 정규화
A = full(sprand(N, N, D_avg/N));
A(A~=0) = (A(A~=0) - 0.5) * 2;
A = A * (Spectral_Radius / max(abs(eig(A))));
% W_in 생성 (Random Uniform [-sigma, sigma])
Win = (rand(N, input_dim) - 0.5) * 2 * sigma;
%% Reservoir state 계산
% r(t + dt) = (1 - alpha)*r(t) + alpha * tanh(A*r(t) + Win*u(t) + xi)
total_steps = size(train_x, 1);
states = zeros(total_steps, N);
r = zeros(N, 1);
for i = 1:total_steps
linear_part = A*r + Win*train_x(i, :)' + bias_scale;
r = (1-alpha)*r + alpha*tanh(linear_part);
states(i, :) = r';
end
%% Delta_R, Delta_S 설정
beta_reg = 1e-8; % Ridge regression parameter
R_raw = states';
S_raw = train_y';
r_bar = mean(R_raw, 2);
s_bar = mean(S_raw, 2);
delta_R = R_raw - r_bar;
delta_S = S_raw - s_bar;
%% 출력 가중치 W_out* 및 c* 계산
% W_out* = delta_S * delta_R^T * (delta_R * delta_R^T + beta * I)^-1
term1 = delta_S * delta_R'; % (P x N)
term2 = (delta_R * delta_R') + (beta_reg * eye(N)); % (N x N)
W_out = term1 * inv(term2); % 역행렬 곱
% c* = - [W_out* * r_bar - s_bar]
c_star = - ( (W_out * r_bar) - s_bar );
test_len_actual = size(test_x, 1);
test_states = zeros(test_len_actual, N);
for i = 1:size(test_x, 1)
% 1. Test 입력 가져오기
u = test_x(i, :)';
% 2. Reservoir 상태 업데이트 (학습 때와 동일한 식)
linear_part = A*r + Win*u + bias_scale;
r = (1-alpha)*r + alpha*tanh(linear_part);
% 3. 상태 저장
test_states(i, :) = r';
end
% 예측 수행
Y_pred = (W_out * test_states' + c_star)'; % (P x Test_Time)' -> (Test_Time x P)
%역변환
Y_pred_real = (Y_pred .* sigma_y) + mu_y;
% 결과 비교
figure('Position', [100, 100, 1000, 600]);
% y 변수 비교
subplot(2,1,1);
plot(raw_test_y(:,1), 'b', 'LineWidth', 1.5); hold on; % 원본 실제값
plot(Y_pred_real(:,1), 'r--', 'LineWidth', 1.5); % 역변환된 예측값
title('Inference of y');
legend('Real', 'Inferenced'); grid on;
xlabel('Time Step'); ylabel('y');
% z 변수 비교
subplot(2,1,2);
plot(raw_test_y(:,2), 'b', 'LineWidth', 1.5); hold on; % 원본 실제값
plot(Y_pred_real(:,2), 'r--', 'LineWidth', 1.5); % 역변환된 예측값
title('Inference of z');
legend('Real', 'Inferenced'); grid on;
xlabel('Time Step'); ylabel('z');
최종 수정 : 2026/02/07
'Research' 카테고리의 다른 글
| Reservoir computing - Hyperparameter optimization 실습 (MATLAB) (0) | 2026.01.31 |
|---|---|
| Bayesian Optimization에 대한 컨셉 이해 & MATLAB 실습 (0) | 2026.01.31 |
| Next Generation Reservoir Computing 코드 실습 (MATLAB) (0) | 2026.01.31 |
| Next Generation Reservoir Computing 읽기 (0) | 2026.01.25 |
| 레저버 옵저버 (Reservoir observer) 논문 읽기 (1) | 2026.01.24 |




