기억보다 기록을
Next Generation Reservoir Computing 읽기 본문
Next Generation Reservoir Computing (NG-RC) 에 대해 알아보자.

Reservoir computing (RC)의 고질적인 문제점은...
- 행렬 \( A \)나 \( W_{in} \) 을 랜덤하게 설정했기 때문에 성능이 들쭉날쭉함
- \( \alpha \) 등의 parameter 값에 따라 성능이 달라지기 때문에 tuning하는데 드는 cost가 많았음

그래서 저자들이 NG-RC를 소개하며 이야기하고 싶은 것이 무엇인가?
- RC에서처럼 행렬을 랜덤하게 만들어서 학습할 필요 없이, Time-delayed data와 약간의 nonlinear term정도만 가지고도 좋은 성능을 낼 수 있다
- 기존의 RC에서 parameter tuning에 소요가 많이 들었던 반면 NG-RC는 그 정도가 덜하다
- 사실은 기존의 RC도 Nonlinear Vector AutoRegression (NVAR)의 implicit form 였다..
- RC에서 초기 조건의 영향력을 없애기 위해 날려야하는 앞부분 데이터가 꽤 많았지만 NG-RC는 예열 과정 (warm-up period)이 획기적으로 단축되었다.
- NG-RC로 forecasting을 한다면.. 특정 Lyapunov time까지의 short term prediction은 아주 잘 working한다

기존의 RC 수식을 보자.
$$ \mathbf{r}_{i+1} = (1 - \gamma)\mathbf{r}_i + \gamma f(\mathbf{A}\mathbf{r}_i + \mathbf{W}\mathbf{X}_i + \mathbf{b}), $$
여기서 \( A \)는 node간의 adjacency matrix이고, \( \gamma \)는 leakage rate, \( W \)는 입력값에서 reservoir layer로 보내는 weight matrix, \( b\)는 bias term, \( f \)는 일종의 activation function 역할을 한다 (2번 논문 참고).
Tikhonov regularization (Ridge regression)을 통해 output weight matrix인 \( W_{out}\)을 구하고,
출력값인 \( Y \)를 feature vector인 \( \mathbb{O} \)와의 연산을 통해 계산했다.
$$ \mathbf{Y}_{i+1} = \mathbf{W}_{\text{out}}\mathbb{O}_{\text{total},i+1}, $$
참고로 2번 논문에서는 \( f(x)=\text{ tanh }(x)\)를 사용했고, \( \mathbb{O}_{\text{total}, i} = r_i\)를 사용했다.
$$ \hat{\mathbf{s}}(t) = \mathbf{W}^*_{out}\mathbf{r}(t) + \mathbf{c}^*, $$
이 논문의 저자들은 \( \mathbb{O_{\text{total}}} \)을 굳이 linear로 한정하지 말고, nonlinear term까지 추가해서 써보자! 라고 제안한다.
예시로 저자들은 Hadamard product를 사용하여 \( \mathbb{O_{\text{total}}} \) 을 linear term & nonlinear term을 concatenate한 큰 덩어리로 변형했다.

예를 들어서 time step이 \( T\)개 있고, \( r(t) \in \mathbb{R}^N \)이라면 (4)번 수식에서 \( \mathbb{O_{\text{total}}} \) 의 형태는 다음과 같다 :
$$
\mathbb{O}_{\text{total}} =
\begin{bmatrix}
r_{1,1} & r_{1,2} & \cdots & r_{1,N} & r_{1,1}^2 & r_{1,2}^2 & \cdots & r_{1,N}^2 \\
r_{2,1} & r_{2,2} & \cdots & r_{2,N} & r_{2,1}^2 & r_{2,2}^2 & \cdots & r_{2,N}^2 \\
\vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots \\
r_{T,1} & r_{T,2} & \cdots & r_{T,N} & r_{T,1}^2 & r_{T,2}^2 & \cdots & r_{T,N}^2
\end{bmatrix}
$$
그럼 다음으로 생기는 질문은, linear term인 \( \mathbb{O_{\text{lin}}} \) 과 nonlinear term인 \( \mathbb{O_{\text{nonlin}}} \) 을 어떻게 구성할것인가? 이다
저자들은 linear feature를 time-delayed component로부터 구성했는데, 이 지점에서 parameter \( k\)와 \( s \)가 등장한다.
- \(k \) : Number of delays. 과거를 몇개나 볼 것인가? (ex : \( k=2 \)면 현재와 바로 직전 정보만 사용)
- \(s \) : Number of stride. 데이터 간격 (ex : \( s=5\)면 \(t, \, t-5, \, t-10, \cdots \) 데이터 사용)
그래서 만약 입력값이 \( d \)차원이라면, linear term은 매 타임스텝마다 \( d \times k \) 크기의 벡터가 된다.
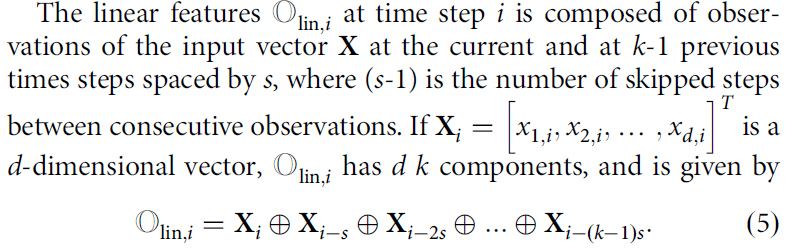
이론적으로는 퍼포먼스를 향상시키기 위해서 \( k \)의 값을 infinite하게 둬야하지만,
실제로는 Volterra series의 매우 빠른 수렴 속도 덕분에 작은 값의 \( k\)로도 우수한 퍼포먼스를 낸다고 한다.

다음으로 nonlinear feature vector를 어떻게 구성할 것인가? 에 대한 질문이 남는다.
마치 SINDy에서 trigonometric function, polynomial, logarithmic function 등 다양한 선택지를 놓고 시스템을 가장 잘 표현하는 최적의 라이브러리(Library)를 구성하듯이 원하는만큼 비선형 함수를 나열 할 수도 있지만,
저자들은 낮은 차수의 polynomial만 써도 충분하다! 라고 주장한다

\( \mathbb{O}_{\text{nonlinear}}^{(P)} \) 를 linear term을 P번 outer product한 행렬로 정의하자.


\( \mathbb{O_{\text{lin}}} \) 이 길이가 \( d k \)이기 때문에 outer product에서 중복된 term을 제거하면 \( \mathbb{O}_{\text{nonlinear}}^{(2)} \) 의 길이는 upper triangle의 원소 개수인 \( (dk)(dk+1)/2 \)가 된다.
예를 들어서 \( \mathbb{O_{\text{lin}}} \)의 원소 개수가 3개라면,
$$
\mathbb{O}_{\text{lin}} =
\begin{bmatrix}
a \\
b \\
c
\end{bmatrix}
$$
외적을 한 형태는 다음과 같이 생기고,
$$
\begin{bmatrix}
a \\
b \\
c
\end{bmatrix}
\times
\begin{bmatrix}
a & b & c
\end{bmatrix}
=
\begin{bmatrix}
\mathbf{a^2} & \mathbf{ab} & \mathbf{ac} \\
ba & \mathbf{b^2} & \mathbf{bc} \\
ca & cb & \mathbf{c^2}
\end{bmatrix}
$$
upper triangle의 원소만을 모아서 나열하면 \( \mathbb{O_{\text{lin}}} ^{(2)}\) 는 다음과 같이 생긴다.
$$
\mathbb{O}_{\text{nonlinear}}^{(2)} =
\begin{bmatrix}
a^2 \\
ab \\
ac \\
b^2 \\
bc \\
c^2
\end{bmatrix}
$$
이렇게 구축한 feature vector들을 다 concatenate해서 최종적으로 만든 \( \mathbb{O}_{\text{total}} \)와 Ridge regression을 통해 찾은 \( W_{out} \) 을 통해 최종적으로 원하는 타겟 변수를 추론한다.
$$ \mathbb{O}_{\text{total}} = c \oplus \mathbb{O}_{\text{lin}} \oplus \mathbb{O}_{\text{nonlin}} $$
$$ \mathbf{X}(t + dt) = \mathbf{W}_{\text{out}}\mathbb{O}_{\text{total}}(t) $$
RC 대비 NG-RC의 장점 중 하나는, 워밍업에 필요한 데이터 수가 아주 적다는 것이다.
RC의 경우 초기 조건의 영향력을 없애기 위해 약 \( 10^3 \) 개 이상의 데이터를 버려야했지만,
NG-RC는 feature vector인 \( \mathbb{O_{\text{lin}}} \) 을 구성하기 위해 \( s \times k \)개의 데이터만을 요구한다.
이러한 특징은 데이터가 아주 희소한 문제를 다룰 때 유용하게 쓰일 것으로 기대된다.

또한 NG-RC는 RC 대비 계산 속도가 매우 빠르다고 한다.
Nonlinear Vector Autoregression (NVAR)은 시계열 예측에서 다변수들 간의 비선형 연산을 통해 미래 값을 추정하는 회귀분석 기법이다.
이 논문의 저자 중 한명인 Erik Bollt가 작성한 논문 (3번 논문, 원 논문에서는 18번)에는
"선형 노드를 가진 RC에 비선형 출력(Nonlinear readout)을 달면, 그건 수학적으로 NVAR와 완전히 똑같다."
에 대한 증명이 담겨있다.
덕분에 기존 RC 대비 NG-RC는 고전적 통계 기법인 NVAR 구조를 사용함으로써 Parameter tuning, 행렬 무작위 선정 등에 필요한 computation cost를 획기적으로 줄였다고 한다.

Result 단락에서 저자들은 Lorenz system과 double-scroll system에 대해 NG-RC를 시행한 그림들을 제시했다.
FIG 2는 Lorenz system을 NG-RC로 예측한 결과이다.
이 경우에는 특정 시점까지 \( x,\,y,\,z \) 3개의 정보를 모두 주고 NG-RC를 통해 그 시점 이후를 예측하는 방식을 사용했다.
training phase에서는 실제 값과 모델 예측 값이 아주 잘 맞는 것을 볼 수 있고 (두 곡선이 겹쳐있음),
testing phase에서도 약 5 Lyapunov time까지는 잘 맞추는 것을 볼 수 있다.

FIG 4에서는 Lorenz system에서 \(x,\,y \) 정보를 주고 NG-RC 방법론을 사용하여 \(z \)를 추론한 결과를 나타냈다.
두 곡선이 거의 겹쳐있으니 매우 성능이 우수하다는 것을 확인할 수 있다.

참고문헌
- Gauthier, D.J., Bollt, E., Griffith, A. et al. Next generation reservoir computing. Nat Commun 12, 5564 (2021). https://doi.org/10.1038/s41467-021-25801-2
- Lu, Z., Pathak, J., Hunt, B., Girvan, M., Brockett, R., & Ott, E. (2017). Reservoir observers: Model-free inference of unmeasured variables in chaotic systems. Chaos (Woodbury, N.Y.), 27(4), 041102. https://doi.org/10.1063/1.4979665
- Bollt, E. On explaining the surprising success of reservoir computing forecaster of chaos? The universal machine learning dynamical system with contrast to VAR and DMD. Chaos 31, 013108 (2021).
'Research' 카테고리의 다른 글
| Reservoir computing - Hyperparameter optimization 실습 (MATLAB) (0) | 2026.01.31 |
|---|---|
| Bayesian Optimization에 대한 컨셉 이해 & MATLAB 실습 (0) | 2026.01.31 |
| Next Generation Reservoir Computing 코드 실습 (MATLAB) (0) | 2026.01.31 |
| 레저버 옵저버 (Reservoir observer) 실습 (MATLAB) (0) | 2026.01.24 |
| 레저버 옵저버 (Reservoir observer) 논문 읽기 (1) | 2026.01.24 |




